Procedural Generation in Godot - Part 7: Dungeons (part 2)
Sun, Dec 9, 2018In this series, we’ll explore the applications of procedural generation to game development. While we’ll be using Godot 3.0 as our platform, much of the concepts and algorithms related to this subject are universal, and you can apply them to whatever platform you may be working on.
In this part, we’ll continue working on the random dungeon generator, adding corridors to connect the rooms.
You can watch a video version of this lesson here:
Connecting the rooms
In the last part we created a random collection of rooms, using the physics engine to ensure they are spread out and not overlapping. Now we need to figure out how to connect the rooms together.
There are many different ways to approach this, but we’re going to use the minimum spanning tree (MST) method. Given a set of points (represented as a graph), an MST identifies the minimum number of connections that connects all points with the shortest total path length.
We’ll be using Prim’s Algorithm
to generate our MST. We’ll also use Godot’s AStar node to store the data, as it
is a built-in graph data structure.
Start by adding a variable to store the data in:
var path # AStar pathfinding objectNow in the make_rooms() function, as we cull the rooms, we want to create an
array of the positions of the remaining rooms. We’ll pass this array to the
MST algorithm.
# cull rooms
var room_positions = []
for room in $Rooms.get_children():
if randf() < cull:
room.queue_free()
else:
room.mode = RigidBody2D.MODE_STATIC
room_positions.append(Vector3(room.position.x, room.position.y, 0))
yield(get_tree(), 'idle_frame')
# generate spanning tree (path)
path = find_mst(room_positions)Now we get to where the action happens. See the comments below in the code for a summary of what’s happening. You can read the link above if you’re curious about the details of the algorithm.
func find_mst(nodes):
# Prim's algorithm
# Given an array of positions (nodes), generates a minimum
# spanning tree
# Returns an AStar object
# Initialize the AStar and add the first point
var path = AStar.new()
path.add_point(path.get_available_point_id(), nodes.pop_front())
# Repeat until no more nodes remain
while nodes:
var min_dist = INF # Minimum distance found so far
var min_p = null # Position of that node
var p = null # Current position
# Loop through the points in the path
for p1 in path.get_points():
p1 = path.get_point_position(p1)
# Loop through the remaining nodes in the given array
for p2 in nodes:
# If the node is closer, make it the closest
if p1.distance_to(p2) < min_dist:
min_dist = p1.distance_to(p2)
min_p = p2
p = p1
# Insert the resulting node into the path and add
# its connection
var n = path.get_available_point_id()
path.add_point(n, min_p)
path.connect_points(path.get_closest_point(p), n)
# Remove the node from the array so it isn't visited again
nodes.erase(min_p)
return pathNow we’ll have a path, so all that’s left is to draw it on the screen so we
can see it. We’ll use CanvasItem.draw_line() to draw each connection in the
AStar path.
func _draw():
for room in $Rooms.get_children():
draw_rect(Rect2(room.position - room.size, room.size*2),
Color(0, 1, 0), false)
if path:
for p in path.get_points():
for c in path.get_point_connections(p):
var pp = path.get_point_position(p)
var cp = path.get_point_position(c)
draw_line(Vector2(pp.x, pp.y),
Vector2(cp.x, cp.y),
Color(1, 1, 0, 1), 15, true)Run the game and you should see a beautiful minimum spanning tree connecting your rooms!
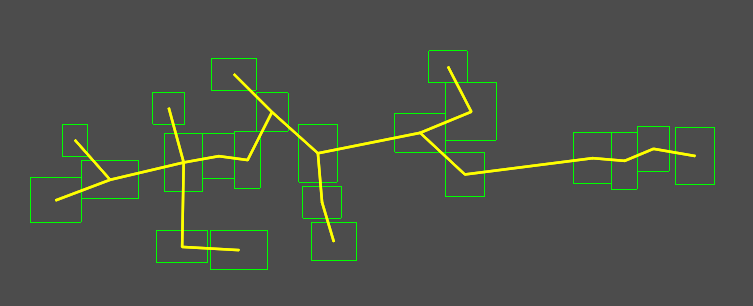
Conclusion
We’re almost there! We have a collection of rooms and a path connecting them. The final step is to convert all of this into a TileMap so that we can actually walk around the dungeon. We’ll do that in the next part.
Please comment below with your questions and suggestions.
